Mixing Differential Equations and Machine Learning
Chris Rackauckas
January 6th, 2020
Neural and Universal Ordinary Differential Equations
The starting point for our connection between neural networks and differential equations is the neural differential equation. If we look at a recurrent neural network:
\[ x_{n+1} = x_n + NN(x_n) \]
in its most general form, then we can think of pulling out a multiplication factor $h$ out of the neural network, where $t_{n+1} = t_n + h$, and see
\[ x_{n+1} = x_n + \Delta t NN(x_n) \]
\[ \frac{x_{n+1} - x_n}{h} = NN(x_n) \]
and if we send $h \rightarrow 0$ then we get:
\[ x' = NN(x) \]
which is an ordinary differential equation. Discretizations of ordinary differential equations defined by neural networks are recurrent neural networks!
Training Ordinary Differential Equations
For the full overview on training neural ordinary differential equations, consult the 18.337 notes on the adjoint of an ordinary differential equation for how to define the gradient of a differential equation w.r.t to its solution. These details we will dig into later in order to better control the training process, but for now we will simply use the default gradient calculation provided by DiffEqFlux.jl in order to train systems.
As a starting point, we will begin by "training" the parameters of an ordinary differential equation to match a cost function. Recall that this is what we did in the last lecture, but in the context of scientific computing and with standard optimization libraries (Optim.jl). Now let's rephrase the same process in terms of the Flux.jl neural network library and "train" the parameters.
First, let's define our example. We will once again use the Lotka-Volterra system:
using OrdinaryDiffEq function lotka_volterra(du,u,p,t) x, y = u α, β, δ, γ = p du[1] = dx = α*x - β*x*y du[2] = dy = -δ*y + γ*x*y end u0 = [1.0,1.0] tspan = (0.0,10.0) p = [1.5,1.0,3.0,1.0] prob = ODEProblem(lotka_volterra,u0,tspan,p) sol = solve(prob,Tsit5()) test_data = Array(solve(prob,Tsit5(),saveat=0.1)) using Plots plot(sol)
Next we define a "single layer neural network" that uses the concrete_solve function that takes the parameters and returns the solution of the x(t) variable. concrete_solve is a function over the DifferentialEquations solve that is used to signify which backpropogation algorithm to use to calculate the gradient. It is a function of the parameters (and optionally one can pass an initial condition). We use it as follows:
using Flux, DiffEqFlux p = [2.2, 1.0, 2.0, 0.4] # Initial Parameter Vector function predict_adjoint() # Our 1-layer neural network Array(concrete_solve(prob,Tsit5(),u0,p,saveat=0.1,abstol=1e-6,reltol=1e-5)) end
predict_adjoint (generic function with 1 method)
Next we choose a loss function. Our goal will be to find parameter that make the Lotka-Volterra solution constant x(t)=1, so we defined our loss as the squared distance from 1:
loss_adjoint() = sum(abs2,predict_adjoint() - test_data)
loss_adjoint (generic function with 1 method)
iter = 0 cb = function () #callback function to observe training global iter += 1 if iter % 50 == 0 display(loss_adjoint()) # using `remake` to re-create our `prob` with current parameters `p` pl = plot(solve(remake(prob,p=p),Tsit5(),saveat=0.0:0.1:10.0),lw=5,ylim=(0,8)) display(scatter!(pl,0.0:0.1:10.0,test_data',markersize=2)) end end # Display the ODE with the initial parameter values. cb() p = [2.2, 1.0, 2.0, 0.4] data = Iterators.repeated((), 300) opt = ADAM(0.1) Flux.train!(loss_adjoint, Flux.params(p), data, opt, cb = cb)
32.33895743168287 11.626035761790217 3.8279028122170042 1.0186999772431977 0.23052507651141854 0.04612786274097307
and then use gradient descent to force monotone convergence:
data = Iterators.repeated((), 300) opt = Descent(0.00001) Flux.train!(loss_adjoint, Flux.params(p), data, opt, cb = cb)
0.042492548405884414 0.04070653643244374 0.03900607872060557 0.03738347043648228 0.03583475604907156 0.034356433857518395
Defining and Training Neural Ordinary Differential Equations
Defining a neural ODE is the same as defining a parameterized differential equation, except here the parameterized ODE is simply a neural network.
Let's try to match the following data:
u0 = Float32[2.; 0.] datasize = 30 tspan = (0.0f0,1.5f0) function trueODEfunc(du,u,p,t) true_A = [-0.1 2.0; -2.0 -0.1] du .= ((u.^3)'true_A)' end t = range(tspan[1],tspan[2],length=datasize) prob = ODEProblem(trueODEfunc,u0,tspan) ode_data = Array(solve(prob,Tsit5(),saveat=t))
2×30 Array{Float32,2}:
2.0 1.9465 1.74178 1.23837 0.577126 … 1.40688 1.37022 1.29214
0.0 0.798831 1.46473 1.80877 1.86465 0.451381 0.728698 0.972098
and do so with a "knowledge-infused approach". To do so, assume that we knew that the defining ODE had some cubic behavior. We can define the following neural network which encodes that physical information:
dudt = Chain(x -> x.^3, Dense(2,50,tanh), Dense(50,2))
Chain(#3, Dense(2, 50, tanh), Dense(50, 2))
Now we want to define and train the ODE described by that neural network. To do so, we will make use of the helper functions destructure and restructure which allow us to take the parameters out of a neural network into a vector and rebuild a neural network from a parameter vector. Using these functions, we would define the following ODE:
p,re = Flux.destructure(dudt) dudt2_(u,p,t) = re(p)(u) prob = ODEProblem(dudt2_,u0,tspan,p)
ODEProblem with uType Array{Float32,1} and tType Float32. In-place: false
timespan: (0.0f0, 1.5f0)
u0: Float32[2.0, 0.0]
i.e. u' = NN(u) where the parameters are simply the parameters of the neural network. We can then use the same structure as before to fit the parameters of the neural network to discover the ODE:
function predict_n_ode() Array(concrete_solve(prob,Tsit5(),u0,p,saveat=t)) end loss_n_ode() = sum(abs2,ode_data .- predict_n_ode()) data = Iterators.repeated((), 300) opt = ADAM(0.1) iter = 0 cb = function () #callback function to observe training global iter += 1 if iter % 50 == 0 display(loss_n_ode()) # plot current prediction against data cur_pred = predict_n_ode() pl = scatter(t,ode_data[1,:],label="data") scatter!(pl,t,cur_pred[1,:],label="prediction") display(plot(pl)) end end # Display the ODE with the initial parameter values. cb() ps = Flux.params(p) # or train the initial condition and neural network # ps = Flux.params(u0,dudt) Flux.train!(loss_n_ode, ps, data, opt, cb = cb)
22.342525f0 1.5856144f0 0.557652f0 0.3702281f0 0.1760086f0 0.10463167f0
The Augmented Neural Ordinary Differential Equation
Note that not every function can be represented by an ordinary differential equation. Specifically, $u(t)$ is an $\mathbb{R} \rightarrow \mathbb{R}^n$ function which cannot loop over itself except when the solution is cyclic. The reason is because the flow of the ODE's solution is unique from every time point, and for it to have "two directions" at a point $u_i$ in phase space would have two solutions to the problem
\[ u' = f(u,p,t) \]
where $u(0)=u_i$, and thus this cannot happen (with $f$ sufficiently nice). However, if we have another degree of freedom we can ensure that the ODE does not overlap with itself. This is the augmented neural ordinary differential equation.
We only need one degree of freedom in order to not collide, so we can do the following. We can add a fake state to the ODE which is zero at every single data point. This then allows this extra dimension to "bump around" as neccessary to let the function be a universal approximator. In code this looks like:
dudt = Chain(...) p,re = Flux.destructure(dudt) dudt_(u,p,t) = re(p)(u) prob = ODEProblem(dudt_,[u0,0f0],tspan,p) augmented_data = vcat(ode_data,zeros(1,size(ode_data,2)))
The Universal Ordinary Differential Equation
This formulation of the nueral differential equation in terms of a "knowledge-embedded" structure is leading. If we already knew something about the differential equation, could we use that information in the differential equation definition itself? This leads us to the idea of the universal differential equation, which is a differential equation that embeds universal approximators in its definition to allow for learning arbitrary functions as pieces of the differential equation.
The best way to describe this object is to code up an example. As our example, let's say that we have a two-state system and know that the second state is defined by a linear ODE. This mean we want to write:
\[ x' = NN(x,y) \]
\[ y' = p_1 x + p_2 y \]
We can code this up as follows:
u0 = Float32[0.8; 0.8] tspan = (0.0f0,25.0f0) ann = Chain(Dense(2,10,tanh), Dense(10,1)) p1,re = Flux.destructure(ann) p2 = Float32[-2.0,1.1] p3 = [p1;p2] ps = Flux.params(p3) function dudt_(du,u,p,t) x, y = u du[1] = re(p[1:41])(u)[1] du[2] = p[end-1]*y + p[end]*x end prob = ODEProblem(dudt_,u0,tspan,p3) concrete_solve(prob,Tsit5(),u0,p3,abstol=1e-8,reltol=1e-6)
t: 62-element Array{Float32,1}:
0.0
0.025993822
0.052559864
0.093415394
0.14211097
0.20731054
0.28383148
0.3714279
0.4711299
0.57710654
⋮
15.756952
16.553768
17.419676
18.367874
19.413296
20.576166
21.882597
23.367315
25.0
u: 62-element Array{Array{Float32,1},1}:
[0.8, 0.8]
[0.7885468, 0.7816014]
[0.77694905, 0.76343244]
[0.75932986, 0.7366743]
[0.7386807, 0.70653033]
[0.7116459, 0.6688899]
[0.6808314, 0.6282734]
[0.64679, 0.5859259]
[0.609661, 0.5423902]
[0.572082, 0.5007786]
⋮
[2.3593026e-5, 1.950222e-5]
[1.3841586e-5, 1.14415625e-5]
[7.7536815e-6, 6.4092533e-6]
[4.110698e-6, 3.397945e-6]
[2.0420862e-6, 1.688005e-6]
[9.378122e-7, 7.7520156e-7]
[3.9127758e-7, 3.2343414e-7]
[1.4493945e-7, 1.1980688e-7]
[4.8657576e-8, 4.0219856e-8]
and we can train the system to be stable at 1 as follows:
function predict_adjoint() Array(concrete_solve(prob,Tsit5(),u0,p3,saveat=0.0:0.1:25.0)) end loss_adjoint() = sum(abs2,x-1 for x in predict_adjoint()) loss_adjoint() data = Iterators.repeated((), 300) opt = ADAM(0.01) iter = 0 cb = function () global iter += 1 if iter % 50 == 0 display(loss_adjoint()) display(plot(solve(remake(prob,p=p3,u0=u0),Tsit5(),saveat=0.1),ylim=(0,6))) end end # Display the ODE with the current parameter values. cb() Flux.train!(loss_adjoint, ps, data, opt, cb = cb)
235.02144f0 38.82619f0 25.955505f0 16.919544f0 10.137426f0 5.733651f0
Partial Differential Equations and Convolutions
At this point we have identified how the worlds of machine learning and scientific computing collide by looking at the parameter estimation problem. Training neural networks is parameter estimation of a function f where f is a neural network. Backpropogation of a neural network is simply the adjoint problem for f, and it falls under the class of methods used in reverse-mode automatic differentiation. But this story also extends to structure. Recurrent neural networks are the Euler discretization of a continuous recurrent neural network, also known as a neural ordinary differential equation.
Given all of these relations, our next focus will be on the other class of commonly used neural networks: the convolutional neural network (CNN). It turns out that in this case there is also a clear analogue to convolutional neural networks in traditional scientific computing, and this is seen in discretizations of partial differential equations. To see this, we will first describe the convolution operation that is central to the CNN and see how this object naturally arises in numerical partial differential equations.
Convolutional Neural Networks
The purpose of a convolutional neural network is to be a network which makes use of the spatial structure of an image. An image is a 3-dimensional object: width, height, and 3 color channels. The convolutional operations keeps this structure intact and acts against this object is a 3-tensor. A convolutional layer is a function that applies a stencil to each point. This is illustrated by the following animation:
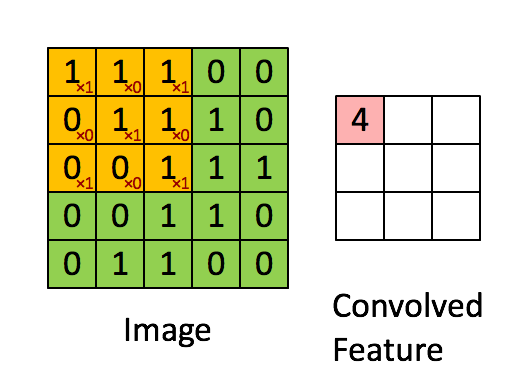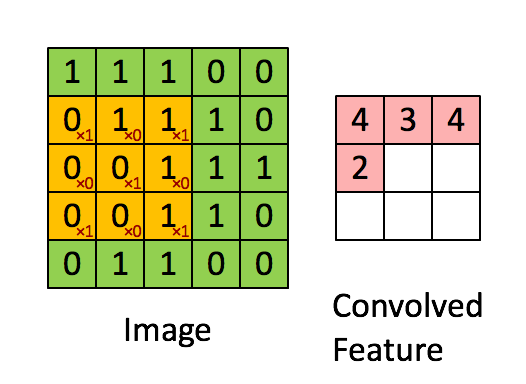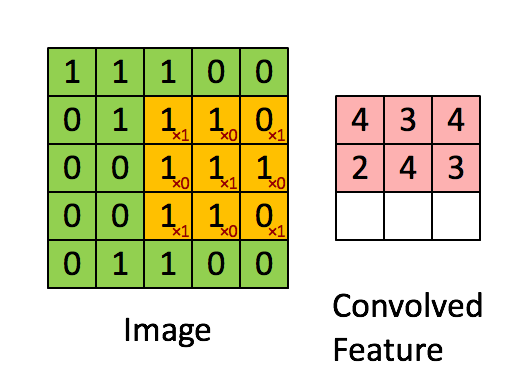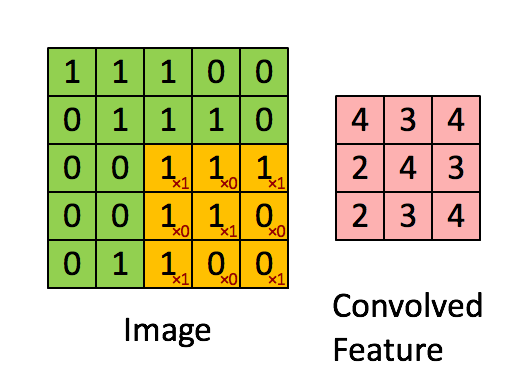
This is the 2D stencil:
1 0 1
0 1 0
1 0 1which is then applied to the matrix at each inner point to go from an NxNx3 matrix to an (N-2)x(N-2)x3 matrix.
Another operation used with convolutions is the pooling layer. For example, the maxpool layer is stencil which takes the maximum of the the value and its neighbor, and the meanpool takes the mean over the nearby values, i.e. it is equivalent to the stencil:
1/9 1/9 1/9
1/9 1/9 1/9
1/9 1/9 1/9A convolutional neural network is then composed of layers of this form. We can express this mathematically by letting $conv(x;S)$ as the convolution of $x$ given a stencil $S$. If we let $dense(x;W,b,σ) = σ(W*x + b)$ as a layer from a standard neural network, then deep convolutional neural networks are of forms like:
\[ CNN(x) = dense(conv(maxpool(conv(x)))) \]
which can be expressed in Flux.jl syntax as:
m = Chain( Conv((2,2), 1=>16, relu), x -> maxpool(x, (2,2)), Conv((2,2), 16=>8, relu), x -> maxpool(x, (2,2)), x -> reshape(x, :, size(x, 4)), Dense(288, 10), softmax) |> gpu
Now let's look at solving partial differential equations. First let's dive into a classical approach. Let's do the math first:
Discretizations of Partial Differential Equations
Now let's investigate discertizations of partial differential equations. A canonical differential equation to start with is the Poisson equation. This is the equation:
\[ u_{xx} = f(x) \]
where here we have that subscripts correspond to partial derivatives, i.e. this syntax stands for the partial differential equation:
\[ \frac{d^2u}{dx^2} = f(x) \]
In this case, $f$ is some given data and the goal is to find the $u$ that satisfies this equation. There are two ways this is generally done:
Expand out the derivative in terms of Taylor series approximations.
Expand out $u$ in terms of some function basis.
Finite Difference Discretizations
Let's start by looking at Taylor series approximations to the derivative. In this case, we will use what's known as finite differences. The simplest finite difference approximation is known as the first order forward difference. This is commonly denoted as
\[ \delta_{+}u=\frac{u(x+\Delta x)-u(x)}{\Delta x} \]
This looks like a derivative, and we think it's a derivative as $\Delta x\rightarrow 0$, but let's show that this approximation is meaningful. Assume that $u$ is sufficiently nice. Then from a Taylor series we have that
\[ u(x+\Delta x)=u(x)+\Delta xu^{\prime}(x)+\mathcal{O}(\Delta x^{2}) \]
(here I write $\left(\Delta x\right)^{2}$ as $\Delta x^{2}$ out of convenience, note that those two terms are not necessarily the same). That term on the end is called “Big-O Notation”. What is means is that those terms are asymtopically like $\Delta x^{2}$. If $\Delta x$ is small, then $\Delta x^{2}\ll\Delta x$ and so we can think of those terms as smaller than any of the terms we show in the expansion. By simplification notice that we get
\[ \frac{u(x+\Delta x)-u(x)}{\Delta x}=u^{\prime}(x)+\mathcal{O}(\Delta x) \]
This means that $\delta_{+}$ is correct up to first order, where the $\mathcal{O}(\Delta x)$ portion that we dropped is the error. Thus $\delta_{+}$ is a first order approximation.
Notice that the same proof shows that the backwards difference,
\[ \delta_{-}u=\frac{u(x)-u(x-\Delta x)}{\Delta x} \]
is first order.
Second Order Approximations to the First Derivative
Now let's look at the following:
\[ \delta_{0}u=\frac{u(x+\Delta x)-u(x-\Delta x)}{2\Delta x}. \]
The claim is this differencing scheme is second order. To show this, we once again turn to Taylor Series. Let's do this for both terms:
\[ u(x+\Delta x) =u(x)+\Delta xu^{\prime}(x)+\frac{\Delta x^{2}}{2}u^{\prime\prime}(x)+\mathcal{O}(\Delta x^{3}) \]
\[ u(x-\Delta x) =u(x)-\Delta xu^{\prime}(x)+\frac{\Delta x^{2}}{2}u^{\prime\prime}(x)+\mathcal{O}(\Delta x^{3}) \]
Now we subtract the two:
\[ u(x+\Delta x)-u(x-\Delta x)=2\Delta xu^{\prime}(x)+\mathcal{O}(\Delta x^{3}) \]
and thus we move tems around to get
\[ \delta_{0}u=\frac{u(x+\Delta x)-u(x-\Delta x)}{2\Delta x}=u^{\prime}(x)+\mathcal{O}\left(\Delta x^{2}\right) \]
What does this improvement mean? Let's say we go from $\Delta x$ to $\frac{\Delta x}{2}$. Then while the error from the first order method is around $\frac{1}{2}$ the original error, the error from the central differencing method is $\frac{1}{4}$ the original error! When trying to get an accurate solution, this quadratic reduction can make quite a difference in the number of required points.
Second Derivative Central Difference
Now we want a second derivative approximation. Let's show the classic central difference formula for the second derivative:
\[ \delta_{0}^{2}u=\frac{u(x+\Delta x)-2u(x)+u(x-\Delta x)}{\Delta x^{2}} \]
is second order. To do so, we expand out the two terms:
\[ u(x+\Delta x) =u(x)+\Delta xu^{\prime}(x)+\frac{\Delta x^{2}}{2}u^{\prime\prime}(x)+\frac{\Delta x^{3}}{6}u^{\prime\prime\prime}(x)+\mathcal{O}\left(\Delta x^{4}\right) \]
\[ u(x-\Delta x) =u(x)-\Delta xu^{\prime}(x)+\frac{\Delta x^{2}}{2}u^{\prime\prime}(x)-\frac{\Delta x^{3}}{6}u^{\prime\prime\prime}(x)+\mathcal{O}\left(\Delta x^{4}\right) \]
and now plug it in. It's clear the $u(x)$ cancels out. The opposite signs makes $u^{\prime}(x)$ cancel out, and then the same signs and cancellation makes the $u^{\prime\prime}$ term have a coefficient of 1. But, the opposite signs makes the $u^{\prime\prime\prime}$ term cancel out. Thus when we simplify and divide by $\Delta x^{2}$ we get
\[ \frac{u(x+\Delta x)-2u(x)+u(x-\Delta x)}{\Delta x^{2}}=u^{\prime\prime}(x)+\mathcal{O}\left(\Delta x^{2}\right). \]
Finite Differencing from Polynomial Interpolation
Finite differencing can also be derived from polynomial interpolation. Draw a line between two points. What is the approximation for the first derivative?
\[ \delta_{+}u=\frac{u(x+\Delta x)-u(x)}{\Delta x} \]
Now draw a quadratic through three points. i.e., given $u_{1}$, $u_{2}$, and $u_{3}$ at $x=0$, $\Delta x$, $2\Delta x$, we want to find the interpolating polynomial
\[ g(x)=a_{1}x^{2}+a_{2}x+a_{3} \]
.
Setting $g(0)=u_{1}$, $g(\Delta x)=u_{2}$, and $g(2\Delta x)=u_{3}$, we get the following relations:
\[ u_{1} =g(0)=a_{3} \]
\[ u_{2} =g(\Delta x)=a_{1}\Delta x^{2}+a_{2}\Delta x+a_{3} \]
\[ u_{3} =g(2\Delta x)=4a_{1}\Delta x^{2}+2a_{2}\Delta x+a_{3} \]
which when we write in matrix form is:
\[ \left(\begin{array}{ccc} 0 & 0 & 1\\ \Delta x^{2} & \Delta x & 1\\ 4\Delta x^{2} & 2\Delta x & 1 \end{array}\right)\left(\begin{array}{c} a_{1}\\ a_{2}\\ a_{3} \end{array}\right)=\left(\begin{array}{c} u_{1}\\ u_{2}\\ u_{3} \end{array}\right) \]
and thus we can invert the matrix to get the a's:
\[ a_{1} =\frac{u_{3}-2u_{2}-u_{1}}{2\Delta x^{2}} \]
\[ a_{2} =\frac{-u_{3}+4u_{2}-3u_{1}}{2\Delta x} \]
\[ a_{3} =u_{1} or g(x)=\frac{u_{3}-2u_{2}-u_{1}}{2\Delta x^{2}}x^{2}+\frac{-u_{3}+4u_{2}-3u_{1}}{2\Delta x}x+u_{1} \]
Now we can get derivative approximations from this. Notice for example that
\[ g^{\prime}(x)=\frac{u_{3}-2u_{2}-u_{1}}{\Delta x^{2}}x+\frac{-u_{3}+4u_{2}-3u_{1}}{2\Delta x} \]
Now what's the derivative at the middle point?
\[ g^{\prime}\left(\Delta x\right)=\frac{u_{3}-2u_{2}-u_{1}}{\Delta x}+\frac{-u_{3}+4u_{2}-3u_{1}}{2\Delta x}=\frac{u_{3}-u_{1}}{2\Delta x}. \]
And now check
\[ g^{\prime\prime}(\Delta x)=\frac{u_{3}-2u_{2}-u_{1}}{\Delta x^{2}} \]
which is the central derivative formula. This gives a systematic way of deriving higher order finite differencing formulas. In fact, this formulation allows one to derive finite difference formulae for non-evenly spaced grids as well! The algorithm which automatically generates stencils from the interpolating polynomial forms is the Fornberg algorithm.
Multidimensional Finite Difference Operations
Now let's look at the multidimensional Poisson equation, commonly written as:
\[ \Delta u = f(x,y) \]
where $\Delta u = u_{xx} + u_{yy}$. Using the logic of the previous sections, we can approximate the two derivatives to have:
\[ \frac{u(x+\Delta x,y)-2u(x,y)+u(x-\Delta x,y)}{\Delta x^{2}} + \frac{u(x,y+\Delta y)-2u(x,y)+u(x-x,y-\Delta y)}{\Delta y^{2}}=u^{\prime\prime}(x)+\mathcal{O}\left(\Delta x^{2}\right). \]
Notice that this is the stencil operation:
0 1 0
1 -4 1
0 1 0This means that derivative discretizations are stencil or convolutional operations.